16++ Applications Of Fourier Series In The Science And Technology Fields Ideas
Applications of fourier series in the science and technology fields. In physics and engineering expanding functions. Thats best faster transmission and processing can be got from fourier series. Fourier Series and Numerical Methods for Partial Differential Equations is an ideal book for courses on applied mathematics and partial differential equations at the upper-undergraduate and graduate levels. The Fourier analysis was originally developed to solve a particular PDE namely the heat equation about 200 years ago. So one of many many applications is compression. Signal processing is the significant one among them. Second when fourier series converge they converge very fast. FTS can be applied to a broad diversity of kinds of spectroscopy such as Fourier transform visible spectroscopy Fourier transform infrared-attenuated total reflectance Fourier transform infrared-photoacoustic spectroscopy Fourier transform infrared imaging spectroscopy and Fourier transform ion cyclotron resonance mass spectrometry. Applications of Fourier Series in Electric Circuit and Digital Multimedia Visualization Signal Process of Communication System. Applied the Fourier series to study the fluid dynamic of the free plane jet. Fourier Series In this worksheet we define a number of Maple commands that make it easier to compute the Fourier coefficients and Fourier series for a given function and plot different Fourier polynomials ie finite approximations to Fourier Series. However over the years the Fourier analysis has been shown to be an indispensable tool not only for mathematics but also for many different fields of science and technology and generalized to various different forms.
Applications Fourier series and their extensions have uses in many fields of mathematics and physics. Summary Fourier analysis for periodic functions focuses on the study of Fourier series The Fourier Transform FT is a way of transforming a continuous signal into the frequency domain The Discrete Time Fourier Transform DTFT is a Fourier Transform of a sampled signal The Discrete Fourier Transform DFT is a discrete numerical equivalent using sums instead of integrals that can be computed on a digital computer As one of the applications. Some of the applications of Fourier series and the generalization of Fourier series Fourier transforms. The Fourier transform has many applications in fact any field of physicalscience that uses sinusoidal signals such as engineering physics appliedmathematics and chemistry will make use of Fourier series and Fouriertransforms. Applications of fourier series in the science and technology fields You take a sound expand its fourier series. Fourier transform is well known tool for many applications in the processing of images in many fields of science and technology also in medicine. Applications of the Fourier Series Matt Hollingsworth Abstract The Fourier Series the founding principle behind the eld of Fourier Analysis is an in nite expansion of a function in terms of sines and cosines. Also the Fourier Transform which is very related to the Fourier Series is used in the Spectrum Analysis of signals. Fourier series such that as the FFT Fast Fourier Transform Discrete Fourier Transform DFT are particularly useful for the fields of Digital signal Processing DSP and. You can separate a song into its individual frequencies boost the ones you care for. Fourier transforms are obviously very essential to conduct of Fourier spectroscopy and that alone would justify its importance. In this paper a spectral method using the Fourier series expansions is used to solve the buoyant two-dimensional laminar vertical jet of a conducting fluid in a magnetic field. Fourier analysis used as time series analysis proved its application in Quantum mechanics.
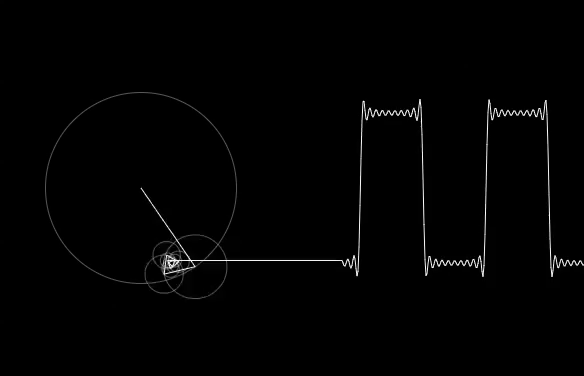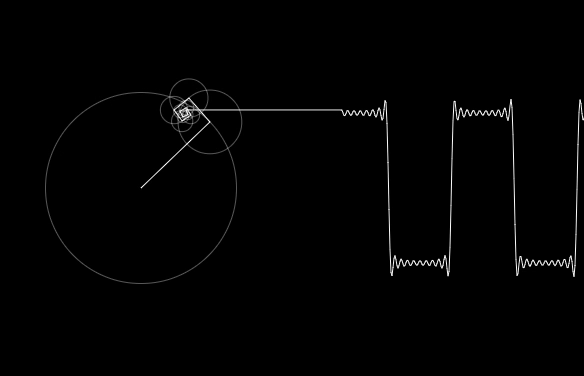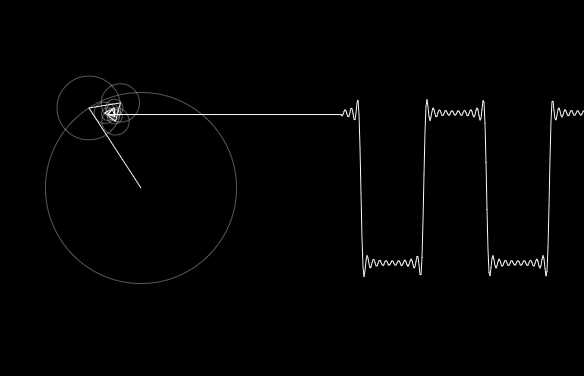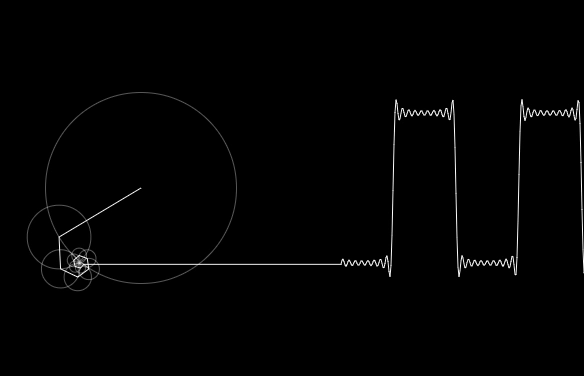Fourier Transformation For A Data Scientist Kdnuggets
Applications of fourier series in the science and technology fields Everyones favorite MP3 format uses this for audio compression.
Applications of fourier series in the science and technology fields. Fourier series is used in computer science in transmission and processing of digital signalsSuppose a digital signal may have a frequency of 200Hz. Signal processing Image Processing and filters representation Data Processing and Analysis and many more. Fourier transform is one of the brilliant algorithms and it has quite a lot of use cases.
Here are some use cases. The really cool thing about fourier series is that first almost any kind of a wave can be approximated. In this case the image processing consists in spatial frequencies analysis of Fourier transforms of medical images.
Introduction and Background Information In the mideighteenth century physical problems such as the conduction pat terns of heat and the study of vibrations and oscillations led to the study of Fourier series. However its rise and fall rates are very much faster than would be expected at 200Hz sine web format. Fourier series expansions have been used to investigate and to form a basis of different topologies comparison to discover their advantages and disadvantages and to determine their control.
In this chapter we discuss modulation strategies of DCMLI and CHBMLI solve their harmonics spectra analytically and compare them using harmonic distortion indices. One of the primary uses occurs in the fields of differential equations especially certain kinds whose solutions are sinusoidal in nature. It would be impossible to give examples of all the areas wherethe Fourier transform is involved but.
Fourier Series are used in the resolution of Partial Differential Equations which appears in many Mechanical Engineering problems such as Heat Diffusion Wave Propagation and Fluid Mechanics problems. The usage of Fourier series makes the route to the solution cleaner and often simpler mathematically.
Applications of fourier series in the science and technology fields The usage of Fourier series makes the route to the solution cleaner and often simpler mathematically.
Applications of fourier series in the science and technology fields. Fourier Series are used in the resolution of Partial Differential Equations which appears in many Mechanical Engineering problems such as Heat Diffusion Wave Propagation and Fluid Mechanics problems. It would be impossible to give examples of all the areas wherethe Fourier transform is involved but. One of the primary uses occurs in the fields of differential equations especially certain kinds whose solutions are sinusoidal in nature. In this chapter we discuss modulation strategies of DCMLI and CHBMLI solve their harmonics spectra analytically and compare them using harmonic distortion indices. Fourier series expansions have been used to investigate and to form a basis of different topologies comparison to discover their advantages and disadvantages and to determine their control. However its rise and fall rates are very much faster than would be expected at 200Hz sine web format. Introduction and Background Information In the mideighteenth century physical problems such as the conduction pat terns of heat and the study of vibrations and oscillations led to the study of Fourier series. In this case the image processing consists in spatial frequencies analysis of Fourier transforms of medical images. The really cool thing about fourier series is that first almost any kind of a wave can be approximated. Here are some use cases. Fourier transform is one of the brilliant algorithms and it has quite a lot of use cases.
Signal processing Image Processing and filters representation Data Processing and Analysis and many more. Fourier series is used in computer science in transmission and processing of digital signalsSuppose a digital signal may have a frequency of 200Hz. Applications of fourier series in the science and technology fields
